極端な話だが，もし対象に一つの差異をも見出せないときは，実は対象自体を見失っている可能性もある．

　 記号の世界では，0と1があれば差異の存在を表せる．差異のある2つの対象から1つを選ぶのに必要な情報量をビット（ｂｉｔ）と名付け，この判別の光速に迫る展開が現在のデジタル革命を導いた．この展開は，「塵も積もれば山…」から，着実な質の追及へと移りつつある．言語機械は，言葉を解釈し，関連づけ，パターンを見出し，新たな組み立てを提示する．

演算や情報伝達のスピードはおかげで速くなるばかりだが，人間の理解のスピードは一向に上がらない．むしろその状況の変化に人間性が振り落とされかねない．

だが考えるまでもなく，元々人間は，情報処理においては天賦の才をもつ．言葉を話し，理解し合い，詩や歌を詠み，人生を築いてきた．まさに差異の織りなす極みである．そう自覚するのは希なことではあるが，当たり前の日常に差異の亀裂が入り，表現として客観性を得たとき，自己への洞察と変革が止めどなく始まる．

PageTop

　「同じ」とは，異なる（差異がある）対象に，同じ成分量や性質が含まれるということだ．AとBが同じであるならば，そもそもAとBに分けた理由は何であるか？それを明示しないと，A=B とはなんとも得手勝手な方便となってしまう．AとBに分けた理由は，例えば位置の違いや時の違いなどで、異なる集合や時空として認識できたからだろう．

　では，同じと思われる対象に差異のある性質が含まれる場合は，何と言うだろう？対象は，複数の要素や要因からなるとか，多様性，複合性をもつなどと言うことになる．

例えば，かたちを見る場合に，同じ肉体に属する骨と筋肉は，全く異なる形質（形態と性質）に見える．ここに脊椎動物の美の秘密ありといったところだが，多様な関節や腱や靭帯などもあり，肉体表現の面白さ（難しさ）には事欠かない．

　四肢という言葉があるように，我々の視覚は，すぐに肢体の中に同一性を発見し，それを同型の要素と位置づけて，その多様な状態をまとめて次の認識への足掛かりとしてしまう．四肢の対称性や動きの変化に注目するわけだ．この対称性の発見は，動きの状態や細部の差異へと目を向けるゆとりをもたらす．足，指，爪などの形質や相互の向き合い方の比較と分類だ．

これらを現代科学的に解明しようとすれば，バイオインフォマティクス（bioinformatics）のように生物学や情報科学や統計学を駆使しなければならないようだ．分類学，体系学，進化分類学，数量分類学，分岐分類学などと共に，分子レベルの系統解析も必要らしい．

　はてさて，そうは言っても，静かな山道を一人歩けば，熊に襲われかねないのが現実．ネットには，銀行を装う偽リンク付の詐欺メールも飛び交う．瞬時に対称性をパターン認識し，連関する出来事を想定することで，「食う，食われる」を見分ける本能と直観を，日々研ぎ澄ませておかねば，学問すらおぼつかない．

　差異を見分けてこそ多様に惑わされず，同一性の中に個性をも見出せる．「捨てても捨てても捨てきれないのが個性」などと言う人もいる．柔軟な認識は，固定観念とはならず，状況に応じた枠組みの中で，深い洞察力と創造性を発揮することになる．「やわらかい図学」も幾何学に閉じ籠らないこのような立ち位置にある．

PageTop

「車内の向かいの座席には，母親の右に女の子，一人空いてその右には，いま乗ってきたばかりの青年が，雨に濡れたメガネを大切そうに拭いている．彼の右隣は，相変わらずケイタイに夢中のOL風の女性だ…」と書けば，窓を背にした座席順に一対一対応となる乗客の様子を描写できる．

　少々乱暴だが，この方達にいきなり番号を振って記録する方法もある．数詞は順番と数量を表すだけの意味しか与えられていないので，下記のような構文
順番）＝数詞＋助数詞＋の＋名詞　で簡潔に表せば，
１）一人の母親．　２）一人の女の子．　３）一つの空席．　４）一人の青年．　５）一人のOL
となり，これも順番に一対一対応の配列データとなる．普及しているコンピュータプログラムの配列データは，この形式が多用されるが，これでは空気は読めない．

　自然言語と人工言語（コンピュータ言語）では，表現力にまだ大きな差がある．それを補うのが，期待しない「やわらかい図学」の発想だ．音楽の楽譜も，音程や音価が音符に対応して定められるが，その希薄な内容の解釈方法は実に柔軟で，そのわずかな情報から空気を醸し出す演奏者の才能は，誰もが知るところだ．

　通常，数字や文字記号は，なんらかの方法で具体的に対応する位置と場をもつことで，記憶されている．記憶とは，繰り返し確認できる物質の状態から生じ，この状態を維持し，感知するには，対応する物理的な記憶場所が必要となる．だから記憶装置は，どんなに小さくなっても，沢山のビットをしまう物理的大きさが必要となる．
　紙の上に文字や記号を書く場合は，筆跡を含めた情報がある．文字列の意味だけでなく多くの筆跡情報が紙面に付着して並ぶことになる．分子単位で見れば膨大な情報量なのだが，それを人の眼は反射した光で受け止め，瞳孔と水晶体で調整し，適度に反応した網膜細胞を脳から文字記号と照合しながら順番に読み取ってしまう．まさに誰もが情報処理の天才で，驚異的な対応能力を持続しているのだ．したがって，数えるなどという単純な「脳作業」は，朝飯前にして眠くなるのだろう． だからオオカミも…と言って笑い飛ばしたいところだが、脳の中では、羊とオオカミでは大違い．そこを同じ数だと割り切るのが，数学的抽象の冷徹さなのだろうが，「やわらかい図学」は優柔不断で，空気を読むことも受け入れる．　PageTop

かたちの要素と座標符

　形譜におけるかたちの要素とは，表現体を形成する大よそのパターン（型）である．

　一般的な人間の視覚において，表現体である対象全体から，かたちの要素を見出すことはたやすい．対象が樹木ならば，繰り返される枝振りや枝の葉の並び，そして大よその葉の形がその要素となる．脊椎動物ならほぼ左右相称の頭部と胴と尾，そこから伸びる前肢と後肢をもち，更に見かけ上は異なる指や爪や蹄といった要素が見られる．それらは，多くの筋肉によって囲むように結び付けられ，その周りを脂肪と表皮が覆うことにより，複雑な構成を滑らかで一体感のある肢体へと変容させている．自然形態には，要素をひとつのかたちと見なせば，さらに，その中にまた要素のかたちが見えるような階層的構造が見いだせる．これらをどこまで詳細に表現し，下層部で技法的要素（絵筆のタッチやヘラやノミの調子，あるいは，表現素材の肌理）へと回帰させるかが表現技法の面白さの一面でもある．

　かたちの要素は，光源のかたちの大よその指定も可能である．造形作品をどのような光の空間に位置づけるかを指定できる．

　立体イメージの可視化の方法は，個人のデッサン力に負うところが大きいが，CG（コンピュータグラフィック）の3次元データの可視化処理技術も進み，レンダリング（描写）処理によって写真のようなレベルの表現を素早く表示できるようになった．人手で描くよりも圧倒的な速さであり，高度なオープンソフトすらある．しかし，人間のもつ身体性は，そう簡単に放棄するわけにはいかないのだ．ひどく手間のかかる正確なモデリングや立体イメージの可視化においては，彫刻の星取りに代る3次元測定やCAD,CAM,CAEの活用が普及していくであろう．だが，その表現力が手業を上回ることは困難と思われる．芸術的表現としては，構成を記譜した形譜を介して，制作家の手業へと引き渡す方が表現力もまさる．人間の尊厳において，これは機械に譲りがたいところである．生きている己の身体性を自らの意思で放棄することは，自殺行為に近いのだ．なぜ都心でマラソンが流行るのか…？その答えもここにある．これは，動物性から疎外された人間達の非暴力的デモンストレーションなのだ．

　制作者自身の輪郭への解釈を尊重するため，形譜に輪郭線や輪郭面を明確にしない方法もある．形譜の座標符による表現は，存在する対象の境界面を点による大まかな位置として表しており，それを線で結ぶのは，表象として現れるであろう大よその面の連なりを解りやすく表示するためである．したがって，形譜を実制作として表現する場合には，実制作者（パフォーマー）が作品の置かれる場の状況や，形譜の解釈とその表現技法とを統合的に掌握していることが必要となる．これは，楽譜で表記される楽曲をどのように演奏するかと同様である．

　形譜で絵画的平面表現を記譜する場合には，かたちの要素の表現方法は，絵画の素描（線画）に相当する．この場合には，輪郭線やハッチングによる陰影，グラデーションといった，暗黙的（文法的）了解による線描の技法が伴う．したがって，形譜で絵画的構成を表現する場合には，平面表現に特有の法則性への配慮や，その表現方式の記載が必要となる．事実，これらの技法は，ベクトルデータによるグラフィックデザインソフトにも受け継がれ，実制作時の一般的ツールとしてさまざまな工夫がなされて普及している．だが，あつかえるインターフェイスや表現素材が限定されるため人間的技量が発揮できにくく，その表現力は伝統的な技法に及ばない．形譜の確立によって，これらのベクトルデータも，タブーや偏見が薄れるなかで，実制作者の解釈へと委ねられ，熟練した手業と多彩な素材によるパフォーマンスへと引き継がれることになるだろう．

つまり，作曲家のように，造形作家は，的確な表現によって，作品の要素を構成し形譜を記述することで，実制作者（パフォーマー）の多様な解釈と表現力を引き出すことが可能となるのである．

　かたちの要素をいま少し基本的観点から見ると，要素を線で表す場合には，その対象を何らかの条件で周りの空間から区切って認識している。しかし，網膜上の内的対象は，外的対象を写した写真を拡大してみても分かるように，その境目に線などはない．つまり，いわゆる輪郭線と称するものは，対象と場（空間や背景）との境目に想定された仮想の境界面の輪郭をあらわしている．線の幾何学的定義は、点の軌跡であり，点は位置があっても面積はないのだから，線も幅がなく見えるものではない．つまり、具体的に表現された線とは，脳内の抽象概念や想念の可視化なのであり，具体的に線を表すときには，幅が必要である．つまり，細長い面をなんらかの技法で色塗りすることになるわけだ．だとすれば，造形表現における輪郭にはどのような表現が相応しいのであろうか？美術を振り返れば，その輪郭や線の描き方には実に様々な工夫が見えてくる．美術史はパターン認識の歴史でもあるからだ．

図★フェルナン・レジェ　『ピクニック』　

　絵画のような平面表現の造形譜は，すでに試みられてきた下絵などの手法も参考にすべきである．下絵といえども線の太さやタッチの相違により，その情報量は大きく変化する．これをできるだけ構成的要素として簡潔な表現にしない限り，パフォーマンスの領域が解放されない．この兼ね合いは，絵画表現の多様な形式を考慮すると，実は座標符だけでは難しい．少々解像度が低くともスケッチのような画像データの方がかえって融通が利く簡便な表現となる．この書式は，具体的な事例によって情報の引き渡しどころを探りだす以外にないようだ．

図★：パウル・クレーの素描『ホフマン風のスケルツォ」1918とそれを下絵とした２つの作品．音楽なら自作自演であるが，作家の中での素描の位置付けは，造形譜の先駈けと言える．引用文献：『パウル・クレー｜おわらないアトリエ』日本経済新聞 2011　　PageTop

共通の要素を見つけ出す

自然の形は多様であり，今では遺伝子レベルでの進化過程が探求されている．しかし，誰もが知る自然形態の多様性は，日常目にする形態をとおしての知見だ．かたちによる博物学的分類は，誰もが小さいころから視覚的に習得している親しみのある手法といえるが，その高度なパターン認識と膨大なデータベースを自認する人は少ない．誰もが天才の故である．

要素の抽象化

かたちの要素は，内的表象から更に抽象化され，分類・整理されていく．それゆえに，たとえば脊椎動物がどのようなポーズをとろうとも，左右の対称性を照合することで，外的対象の差異を内的表象において安定的に同一形態として認識することができる．

図★　数種のポーズと対応する骨格

かたちの抽象レベル

　形譜の構成において，かたちの要素を具象←→抽象のどのレベルで記譜するかは，作品全体の構想にかかわる問題である．3次元の形を記譜するには，点列で線や面を表す．これ等を形典では座標符と名付ける．これは，CADで使われる頂点に近い意味であるが，形典の座標符は，おおよその位置を表し，数学での面積の無い点とは異り近傍での範囲を表す符号となっている．これらの座標符も，後方で述べる配列概念として整理され、CAD等で３D変換可能なオブジェクトとして扱われている．

図★：立方体からのやや詳細な解釈表現．これ等の複合的解釈も成り立つ．前列右端が８頂点よりも精度を上げた立方体の表現となる．
PageTop

要素と要因

　自然形態のかたちのプロセスは，結晶や植物の分岐，ボロノイ図や反応拡散など，そのパターン形成の背後には微細な要素と複雑な要因や仕組み（機構）がある．また，それを可視化する場合にも，各要素の見え方を変化させる光の当たり方とか反射の違いといった物理的要因がある

かたちの要素にはたらく要因

　造形構成において，かたちの要素を配置することをパターン展開（図★）という．これはパターン認識と逆の過程で抽出した要素を展開・配置し，構成の再現性を確認をすることになる．このとき要素に働く移行，回転，拡縮，変形などの作用（図形処理）が構成の要因であり，さらに，質感の付加，色の反射・発光作用などが構成の属性的要因である．もちろん自然形態の記譜の場合，これらの要素と要因による組み立ては，自然の形成過程とは異なる視点であるので，いわば視覚的なかたち合わせや数合わせに過ぎないのだが，視覚的パターン認識の演繹的検証ともなり，形典における重要な客観的視点となる．

　形譜の要素に作用する要因は，極めて客観的なCGの図形処理と考えればよい．したがって，自然科学のビジュアルな物理シミュレーションもかたちの要素の環境要因として適応することが可能である．

　心象として作用するかたちの要因には，たとえば，仏典（法華経）などで言うような，十如是【相（形相）・性（本質）・体（形体）・力（能力）・作（作用）・因（直接的な原因）・縁（条件・間接的な関係）・果（因に対する結果）・報（報い・縁に対する間接的な結果）・本末究竟等相】などのような難解なる観点を欠くことができぬが，これらの統合的イメージは，形譜の解釈や実制作において表現されるべき課題である．もちろん，造形作家の構成には芸術的直観とでも言うべき表現が加わるであろう．果たして形譜からそれが想起できるか否かは，今後の発展の経緯に期待したい．

　近年は，かたちの要素や要因を定量・定性化したものが，CGのプログラム上で機能するようになり，かつては実制作家のレンダリング（描画）にたよっていた透視図法による写実的表現も，写真のようにリアルなCG画像に置き換わってきた．映像製作においても様々な物理的シミュレーションが取り入れられ，実写とCGを合成し，空想のリアルな可視化まで生むに至っている．子供の空想力まで封じてしまう過剰な表現は，『我が子を食らうサトゥルヌス』を観るようでもある．　PageTop

PageTop

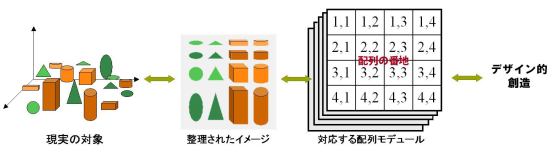
整列された情報

　配列概念とは，ものごとを整理し，解りやすく説明するための記憶形式を意味する．それは，校庭で遊んでいる子供たちが一列に並んだり，ジャングルジムの立体格子にちょうど一人ずつ収まったりした状態で，相互の関係に一定の順序性が付加できる記憶の整理法だ．再び子供たちが校庭に，あるいは社会へと散っていっても，この整理された記憶を基に現状を語ることができる．「ジャングルジムの上から3段目の右端最前列にいた女の子は，今この学校の数学の先生で，その左隣りの男の子も，なんと国語の先生の…．」などとである．

　表計算ソフトの表や住所録ソフトでも同じように情報を整理し，相互の関連を自在に抽出することができるが，実は．これらのソフトウェアープログラム自体も背後で配列変数という同様の記憶形式を活用している．

配列概念は，自由度の高い概念で，その活用は難解となるが，造形譜を創作するうえで大切な概念であり，表現体の分析的探求においても利便性の高い概念モデルである．

形典での“配列の場”とは，配列変数における“配列要素”や表計算における“セル”とおなじ概念だが，形の要素やその配列データとの混同をさけるために“配列の場”と呼んでいる．セルと呼ばない理由は慣習を避けるためと，より抽象的であり，かたちの要素のもつ場とも関係するためだ．

形典では表現体を分析的視点からかたちの要素や要因に分けるが，これを配列の場を対応させて整理すると，配列自体の一体性によって全体の周期や相互の関係性（美的形式：リズムやプロポーション等）を把握することが可能となり，構成を統合的に観る空間的な概念モデルを形成できる．形譜におけるかたちの要素を記号化して配列の場に格納し，その要因としてのリズム，シンメトリー，プロポーションを統合的に配列の場と同期させることで，造形譜の構成的構造を提示することもできる．（図 5 1参照）．

　上記で述べた「かたちの要素」の座標符も配列を使ってデータ化できる．CGで言うオブジェクトであり、ワイヤーフレームモデルやサーフェイスモデルに相当する．書式は、これらを活用した方が使い勝手の良いものとなる．

　表現体を構成する要素を，図 51の配列のように，行，列方向に束ねたとすると，行，列の数を構成の周期性として見立てることができる．現実の対象を整理する場合には，配列数が実体とうまく一致しない複雑さも生じるが，造形モデルとしては、周期性がはっきりと見えるほうがリズムを把握しやすい．

図 51　現実の対象と整理されたイメージ．
　整理されたイメージには， 丸，三角，四角柱，円柱の4種のかたちが4段階の変形をし，16個の要素として配置されている．配列モデュールには，かたちに作用する要因として，移行（位置），回転，拡縮，色彩などを配列モデュールの各層に記録している．

もっと詳しく　配列概念　>>>

数えるための抽象と捨象

　子供たちは，「いち・にぃ・さん…」と元気に数え方を覚える．これは対象の抽象化の学習であり，捨象，つまり個別的な性質を捨て去り，同じ性質だけを取り出す訓練である．あたかも分離できる等価な対象として数1，2，3…を対応させて数えていくわけだ．したがって，人を数えれば何人，鳥なら何羽，猫なら何匹などと数を表す語要素（1，2，3，…）に意味をつなぐ助数詞（単位）をあわせて1つの数詞として抽象度を調整できるわけだ．

集合数と順序数

数は，その対応関係を変幻自在とする巧みな概念操作の核であるが，数には量を表す「集合数」と順序を表す「順序数」がある． PageTop

数と周期

　数に周期があるか？と疑問に思うかもしれないが，人間はたくさんの数の名前（数詞）は覚えられないので，その記数法に明解な周期をもたせている．周期は束ねの繰り返しとも考えられる．束ねた数をまた束ねて階層性を作り出す．二進法なら２の周期，十進法なら10の周期，時刻なら２，１２，２４，６０の周期が使われている．すべてが数えるための暫定的な利用とも言えるが，これがいつの間にか固定観念を作り上げる．１が3で割りきれないのだ．

　ソロバンとは良くできたもので，四つ玉や五つ玉で５進法を組み込むことで，向き合った指による素早い演算操作を可能にし，一目で各桁の0から９の違いが見分けられるようにしている．人と器具の長所を生かし，入出力と演算を同時に行なってしまう実に優れた情報処理システムなのだ．

　ところで，1を3で割り切れないのは，十進法だからであって，三進法ならピタリと割れることになる．だから尺貫法の一間は３で割り切れる．したがって順序の表記も造形構成にしたがった記数法で繰り上がる方が分かりやすいことになる．音楽で１小節を３拍子で割り切れないと思う人はいない．記譜法としては，何拍子でも記述できるようになっている．楽典の方が，一曲を音の集りとして見る場合，度量衡の計量方法より数学的には気が利いているかもしれない．

　ヤードもポンドも12で割れてインチになる．一体いつごろから造形デザインをメートル尺で測るようになってしまったのだろう？それは，グローバル経済のための強引な度量衡の改定からだ．確かに，論理的にも世界的な共通基準が必要だった．

　知見が増せば，絶対的基準も不便なものとなるのは仕方がない．造形活動には尺貫法の１間＝６尺のように２でも３でも割れる記数法も必要なのだ．形譜なら個別の単位系も生まれるだろう．基準の本質は融通無碍であらねばならぬ．コンピュータも普及した．頭の可塑性のためには，そろそろメートル法も，標準時も根拠なき立派な世界基準であることを認める方が，使い勝手の良い単位をローカルに活用できることになる．

　記数法は値と周期をもつ．一定した繰上りの場合は，桁上りごとにその周期が指数的に長くなるといえる．だがRGBの色指定（白なら#ffff）のように，桁ごとに異なる性質の値を表す記号だと考えれば，各桁自体は同じ周期ｆ（=16）であり，その値は組み合わせの差異を表す番号（000～fffで4096色）となる． 　 PageTop

数概念の再確認

目の前の対象を視覚認識で個別に分離して数えられるようになることは，対象を抽象的にとらえる訓練の第一歩だ．やがてそれが，豚肉\200／100g　などという日常的価値観にまで展開され，\100／€などと貨幣の相対価値にまで至って，矛盾の摺り合わせが為替市場で行われる．何とも悩ましい．まだまだ人間は，数の使い方が未熟なのであろう．もう一度“数”の原点に立ち返り，一部の人間の利便性だけではない数の素敵な利用法を見出し，こころの通う新しいコミュニケーションを生み出したいものである．

PageTop

順序と順序交換

　形典での順序とは，一定の基準による並び方の事である．アイウエオ順，いろは順，番号順，先着順など，どんな並びでも良いが，使う側がその順番を覚えていると，より変化を見極めやすくなる．

下駄箱の下足札に序列を意味しないよう「い，ろ，は，…」と書かれていても，誰もがその場所を特定できる．順序とは，誰が使おうが，何に使おうが，その基準となる順序に対する対応関係は自由なのだ．

　数学での序列の関係は，どのふたつの元（集りの中の対象）でも比較できるような順序は全順序 (total order)， あるいは線型順序 (linear order) などと呼ばれ，どちらが大きいとも小さいともいえない場合には半順序（はんじゅんじょ）と呼ぶようだ． 　形典での序列はさほど厳密なものではなく，見かけ上の比較を大まかに見立てて順序とする場合もある．綿１Kgと鉄１Kgでは，見かけ上等しいとは見定め難いだろう．

　順序の統合的把握は数字と文字の対応で考えると解りやすい．
例えば順序を
（１２３）
（２３１）
（３１２）　と入れ替えたとする．これを適当な文字にして入替てみると，
（のした）
（したの）
（たのし）　となり，
その意味は（伸した）（舌の）（楽し）といった具合に，たまたま意味をなしたとしても，順序の位相が順送りであることと離散的な単語の意味との一致は無関係であり，三つの言葉の関連が付くことは偶然だ．

意味のある漢字を入れ替えればどうなるだろう，
（我足知）
（足知我）
（知我足）　となり，文法的問題もあり
アシと読むかタルと読むかは好みだが，意味を持った漢字は入れ替えても想定内の変化だ．

音階なら，
（ドレミ）
（レミド）
（ミドレ）　と歌うと旋律が変化して聞こえるし，順送りになっていることは音律からも直ぐ解る．ここで，最後にもう一度
（レミド）　を繰り返すと，
なんとかおさまりがついて終わる．なぜだろう？

かたちなら
（×・；）
（・；×）
（；×・）
変化の順序が解るかたちなら
（｜／―）
（／―｜）
（―｜／）　となる．

以上，なんとも乱暴だが，このように順序を入れ替えてみると，
・数字のように，序列だけがはっきり認識され，意味を生じない場合，
・かな文字のように組合せから意味を読み取ろうとする場合，
・漢字のように意味の組合せを文法と共に解釈しようとする場合，
・音階のように，すぐに周期を拍子とし，一連の変化を記憶と照合しながら，旋律を感性と連携させてイメージをくみ取ろうとする場合，
・かたちのように（ここではあえて記号をかたちとしてみたわけだが），単純で意味不明のかたちの組合せでも，新たなイメージを見つけ出そうとしたり，変化の様子を漠然と感じ取る場合，

などがあり，順序化（正規化）とその組み換えが情報に及ぼす影響は，それぞれの情報の書式と文法的規則により解釈が異なる．また，配列のような離散的表現であっても，順序が把握できる変化は認識しやすい．

×・；　・；×　；×・　　　　１２３　２３１　３１２
・；×　；×・　×・；　　　　２３１　３１２　１２３
；×・　×・；　・；×　　　　３１２　１２３　２３１
×・；　・；×　；×・　　　　１２３　２３１　３１２
・；×　；×・　×・；　　　　２３１　３１２　１２３
；×・　×・；　・；×　　　　３１２　１２３　２３１

｜／―　／―｜　―｜／　　　　１２３　２３１　３１２
／―｜　―｜／　｜／―　　　　２３１　３１２　１２３
―｜／　｜／―　／―｜　　　　３１２　１２３　２３１
｜／―　／―｜　―｜／　　　　１２３　２３１　３１２
／―｜　―｜／　｜／―　　　　２３１　３１２　１２３
―｜／　｜／―　／―｜　　　　３１２　１２３　２３１　PageTop

順序・乱数・完全方陣

　かたちを配列モデルで集合的にとらえるとき，順序だっているか順序が乱れているか，周期性（periodicity）はあるか，全体のバランスがとれているかなどの性質が見分けられる．これを数に対応させて調べると，順序と対極にあるのが完全方陣であり，周期性の中で順序が変化するが，バランスされていることがわかる．乱数は周期性もバランスもない．人のパターン認識は，感覚的にこれらの分布を見分けることができる．経験的能力なのであろうか？実に不思議で素晴らしいことである．

これらの差異は，いずれにしろ順序を基準として認識される現象であるので，形典では順序の概念の範疇としておく．

もっと詳しく　魔方陣の基礎概念　>>>

移行的変移

　リズムは，主に要素の移行的変位に注目した性質である．

　移行的とは，相似的な要素が移行，回転，拡縮，変形を繰り返すことであり，変位とは，相似的であると認められるような変化を意味する．これは，周期性のなかでの変化ということもできよう．これは深く感性に係ることだが，ここでは客観的記述が可能な事象を取り上げる．

　リズムといえば音楽を思い浮かべる人が多いだろう．音楽では，楽典（musical grammar）によって拍子（周期性）やリズムを簡明に定めている．拍子は明快だが，リズム感には質の問題が伴う．もちろん3拍子の強弱が分かればワルツ形式の曲をイメージできるが，ヨハン・シュトラウスのようにはいかないし，ウィーンフィルのような奏で方ができるわけでもない．造形でも同様で，形式が同じでも，造形作家と実制作家の力量が作品を左右する．

かたちのリズムについて，数学的な視点でその特徴を上げると，
１．順序のリズム，
２．完全方陣のリズム，
３．乱数のリズム
があり，これらの特別な状態から対象となるリズムの位置付けが可能となる．

　では，造形におけるこれらのリズムは，どのようなかたちで認識できるであろう．まずは簡単な構成を例に考えてみよう．　PageTop

造形のリズムの俯瞰

　図 5 2は，リズムを俯瞰するためのイメージ・チャートである． [石垣　健, 『美の科学遊びーMagic Tiles』形の科学会誌, 2007]　扁平な四角錐の要素4×4＝16 個でアイコン（タグ）を構成している．左端の列のアイコン（タグ）は，下端の比率のように四角錐の底面が縦，横方向へそれぞれ1：ｎ の比率で等比級数的に増加する構成となっている．

なぜ真上から見た四角錐を使っているかというと，
１．四角の対応する辺の長さの変化が比較しやすい．
２．底面のプロポーションが矩形であるので特徴を把握しやすい，
３．真上から見た稜線は矩形の対角線として比例による傾きを表しているので同一のプロポーションの配置がすぐわかることになる．
４．陰が付くことで要素の特徴が三角形のリズムとなって差異がよく見える．
というような理由からである．この四つの特徴を意識してチャート全体を見渡すと，要素の縦横のプロポーションの変化が配置のリズムによって全体の雰囲気を大きく変えているのが解るはずである．そして，順序良く並べた左端の列の配置は，これら四つの特徴が目立たずに収まっていることに注目したい．

図 5 2　イメージ・チャート：各アイコン（タグ）は扁平な四角錐の要素16個の集まり．

表 5 1に対応させて四角錐の要素を入れ替えることで，アイコン内の行や列の順序交換によるリズムの変化がわかるはずである．またチャートの縦列のアイコンは，構成の基本リズムが同じであり，プロポーションが変化していることになる．

表 5 1　順序化した4×4 の配列と，その順序交換のバリエーション．

もっと詳しく　リズムの基礎概念　>>>

均衡

　人間のバランス感覚は，そう簡単ではない．アンバランスのバランスなどが良い例だ．正直言って自分でも何故バランスするのか解らないが，何とも心地よい安定感が得られる場合がある．相反する存在が対峙することで，その存在の強度が釣り合うのかも知れない．

バランスをとるには，次項で述べるようにシンメトリーを複合的に扱う方法がある．

乱数でバランスを得るのはどうも解せない．たまたまバランスしたものを選んでいるのだろうが，それなら作為に基づく方が手っ取り早い．もっとも手癖というものは，つい周期性や秩序性を見せてしまう場合がある．そう考えると，乱数も決して投げやりでは作れない繊細なモデルである． 　PageTop

シンメトリー

対称性

　バランスと共に語られる言葉にシンメトリー（対称性）がある．数学的，物理的解説書も沢山ある．しかし，シンメトリーを目視できるやさしい現象と思うと，並進対称，回転対称，左右対称などのありきたりな図解で終わってしまう．形典では，配列を使って簡単にシンメトリーのモデル化を行い，ポリリズムのような同時性をもつ複合的対称性などを提示している．

シンメトリーは視覚対象内の同一性に注目した特徴である．私たちのパターン認識においてシンプルで重要な判別モデルである．

この地球においては，かたちの秩序と無秩序を大よそ見分けるには，同じかたちの存在，つまりシンメトリー（対称性）の有無に注目すればよい．細波や鱗雲のような並進対称，雪の結晶や花のような回転対称，動物に見る左右対称などは，内在する秩序と外界との関係の表れだからだ．形典は，その秩序の因果を問うものではない．視覚的にシンメトリーの状態を見分けることで，その形式の記述法を定めるものである．

なんとも難解な秩序の中で形成される生物のかたちは，重力の影響を受けにくい水中で，卵のようなほぼ球対称から始まる．やがてそれらはウニやヒトデのような放射対象や貝のように堅固な螺旋を形成し，さらに魚のように動的に上下左右の対称性を保ちながら前後の差異を形成する．植物は根を張り，さらに重力に打ち勝って次第に螺旋的分岐を繰り返す．そして，陸上に上がった動物は左右の対称性を駆使して疾走し，明確な前後と上下を形成している．

だが，シンメトリーをもつどのような動物であれ，足やヒレを完全に左右対称に動かすことはまれである．重心移動により対称性を自ら破らなければ，前進もままならないからだ．地上の動物の前後の差異はシンメトリーの破れを誘うかたちなのだろう．歩行は，前傾し，対称性を左右交互に破ることで波動的な歩みを生むわけだ．この姿は，まさにシンメトリーの移行的変位，つまり，リズムそのものと密接な関係がある．

造形表現においても，静的な図解や極端な象徴性を除けば，生物の輪郭を左右対称に描くことはまれである．このような多様な動きを視覚認識するには，明快なシンメトリーの概念モデルとの照合が大変有効であり，舞踏のように複雑な動きをもつ表現も，この概念モデルとの対応で連続性と対称性を保ち，統合的バランスの中で，動的変化を楽しむことがきるのである．

運動中の対称性が崩れれば前のめりや尻餅をついて転倒する．ならばここにもモビールの腕のように大地との動的バランスが働いている．幸いにも，引力は，この大きな地球に人々を釘付けにすることもなく，遠心力で宇宙へと放り出すこともしない．このおかげでコトコトと歩けると思うと，なんともうれしい限りだ．

このように，森羅万象の動きを瞬時に見分けたり，じっくりと描きこんだりするには，シンメトリーの概念モデルが重要な役割を果たすことになる．もちろん，新たな創造においても，シンメトリーの概念は大いに役立つはずである．　PageTop

シンメトリーと配列表現

　人間のパターン認識は，論理より先行しがちだ．だからこそ，そこに新しい論理性を発見できるのではないかと思いたい．配列の離散的モデルは，風になびく髪と生え際のような関係性を保ち，生え際が糸口となって更に複雑な対称性を対応的に束ねている．

　概念モデルを探るため，配列概念の図 5‑2で現実の対象と整理されたイメージとの対応関係を見ていこう．左端の図のように，現実がどんなに雑然としていても，人の脳内では類型化によって順序良く整理（正規化）できる．更に右の図表のように，定性化・定量化により，要因や属性を多次元的に整理する配列的センスは，誰もがもつ脳の賜物である．

では外界と対応する配列概念の中で，シンメトリーはどのようになっているのだろうか．まず， 表１左端のような2次元の配列に，左上から右下に分かりやすく順序数を配置してみる．ここでは番号を簡便に量的な集合数と考え，その大よそのバランスを見てみよう．この場合，上下・左右に２分割した四つのセットの各々の和は，10，18，42，50 となり，対称性はない．

その右の配列は，配列内の右端の列を左端に送って順繰りに右へずらしてある．この場合， 上の２ セットの各々の和は14， 下の２ セットは46 となり，全体として量的バランスが左右対称に近づいている．

更にその右の3 番目の配列は，左の配列の下端の行を1 行目に上げてずらしてある．この場合は，どのセットも対角線方向の和が30 となり，点対称に近いことがわかる．

最後の右端になると，完全方陣（完全な魔方陣）が生まれている．この場合は，2×２のセットの和も，行も列も斜め方向のセットの和も30 となり，しかも行や列を順送りしてもバランスが崩れない．これは完全方陣と呼ばれ，まさに量的なシンメトリーの極みなのである．

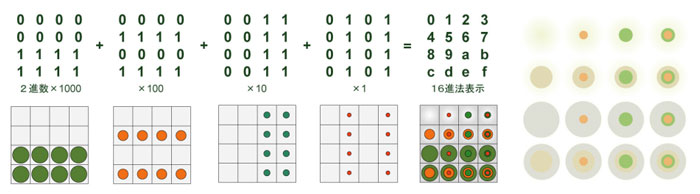
表 3：　順序化した4×4の配列とその順序交換．4進法2桁に変換するとリズムの頁・表1となる．

PageTop

N進表記による配列の対称性

ｎ進法における位取りの表記は，各桁が下位から上位へと周期ｎごとに繰り上がる．この桁上りを無視すれば，周期（種類）ｎをもった数字の配列を表すことになる．

図 5 3は表 5 1の左端の順序の配列を2進法に分解したものである．各桁の値（０か１）の配置を対称性から見るとその分布が良くわかる．この差異の周期性は図 5 4のような波動と見ることもでき，その場合図 5 3は，面的に広がった反応拡散のような周期性をもつ要因と考えることもできる．

つまり値のN進表記による各桁の値は，それぞれ等価な重みをもち，桁ごとのバランスが全体のバランスを形成することになる．

図 5 3　2進法の各桁を配列ごとに分けて表示．0 は白丸のぼかし，１は色の付いた丸印で表現．丸印は桁によって大きさを変えている．

図 5 4 　0 からf（=15）を2進法の各桁の状態を表現したもの．直線的なパルス表示でよいが，各桁の独立的な周期を比較するためにサインカーブとしている．

このように順序の配列と完全方陣の対比で（図★参照）シンメトリーな構成の両極が定まる．その間には，イメージに沿った数多のバリエーションが想定される．そこから秀逸なるものを見出す天才の審美眼とは，なんとも不可思議な天の恵みである．

　さらに見る　シンメトリーの基礎概念　>>>

PageTop

プロポーション

比例的対比

　プロポーションとは，全体対部分，部分対部分の比例的な対比をいう．

　プロポーションは，かたち（構成）のリズム感にアクセントやハーモニーを与える. 音楽で使う和音のような雰囲気もあり，複数の対比により調和的雰囲気が生まれる．だが，和音のように音程の微妙な差異による“うなり”が生じるわけでもなく，感覚的差異を正確に感じ取るのは難しい．目で見るだけで，対象の寸法を言い当てたり，比率を当てられたりする人は希である．とはいえ，調和のあるなしは何となくわかるものだ．

形典でのプロポーションは，かたちの要素の大きさだけではなく，かたちの様々な要因（移行，回転，変形，明度等）に関する比例関係を意味する．これらの比例関係は，微小な変化でも表情のように大きく解釈が異なる場合があり，要素の組合せによっても変化するので，定量化，定性化においては感性に準じた感覚的かつ統合的な順序化（正規化）の調整が必要となる．

同じプロポーションの使用は視覚的なハーモニーをもたらす．ものづくりにおけるプロポーションは，全体対部分，部分対部分の比例に配慮が必要となる．外分と内分が等しい比例，つまり，A=B+C かつA:B=B:Cを満たす比率は黄金比という．線分を２分割するだけで同じ比例関係を２組作れてしまうわけだ．ただし，これを見分けるには若干の慣れも必要だ．

モデュール

　 形典において，造形譜の創作のために必要な統合的概念で，表現体を構築する機能をもった要素や要因の美的形式を規定する概念モデル，及び，それを生み出すシステムを意味する．

これらの概念モデルは，相互に接続可能な配列形式をもつことで組み換えが可能となる．造形的な接続とは，物理的な接続だけでなく，配列形式を同期させることで，リズムやプロポーションなどの交換や調整が可能となる．

０．場の分割のモデュール，　１．かたちのモデュール，　２．リズムのモデュール，　３．シンメトリーのモデュール，　４，プロポーションのモデュール，　５．質感のモデュール，　６．彩色のモデュール，　７．構成のモデュール　等がある．

　４，プロポーションのモデューの実例として、筆者の作品「FRACTAL SCALE」の使用例を参照されたい．

　　 PageTop