更新:
12/07/13
,
|
|
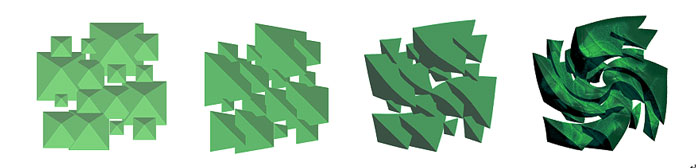
形のリズムと配列表現 リズムと言えば音楽を思い浮かべる人が多いだろう.音楽では,楽典(musical grammar)によって拍子(time)やリズム(rhythm)を簡明に定めている.拍子は時を刻む拍の集まりであり,時間軸に沿った小節の周期的分割を示唆する.3/4拍子などと記され,この場合,音価(一定の時間を刻む音の間隔)を表す四分音符を一拍として3拍を一小節とすることを示唆する.これらの小節が集まって楽節を成し,楽節が集まることで曲の一般的形式が作られている.リズムとは,これらの拍や節の周期性を踏まえた音列の「移行的変位」を意味する.時間軸で拍子を繰り返しながら,拍の強弱,音価の配分,音程(倍音までの音の高さの分割位置),音質(楽器などによる音色)などを吟味し,独特の変化を与え,聞き手に特徴的な感覚を繰り返し呼び起こす現象である. したがって,列方向のアイコンは同じ構成のリズムになっており,行方向は同一のプロポーションの要素で構成されていることになる.視覚認識として,リズムとプロポーションを分離できるだろうか. 音楽とは異なり,造形におけるリズムは,巡る視線により時間軸を折りたたんだような表現空間に展開される.人は,視線移動により変化する視覚認識から,表象としてのリズムを感じ取る.この認識の素早さは,本能的であり,自然形態の同種のパターンの分散を日常的に把握し,異種の形を瞬時に察知することで,環境から身を守る習性と近い関係にある.リズムは,安定した反復によって,動的変化,均衡,対比,調和,をもたらし,感情と密接した複雑で多様な表象を生みだす.数理的モデルから見れば,周期性,順序交換,対称性,比例,階層性などが関係する明解で簡潔な事象が含まれる.多項式などの,周期性のある振る舞いについては他の項目にゆだね,ここでは関連する定数などを含め,離散的な視点からリズムの基本となる“順序の変化(変位)”に注目したい, リズムには柔らかな周期性がある.CGでは,要素となる形やその要因に変化を与えるために乱数が良く使われる.しかし,乱数に周期性はない.リズム化するには,反復したり別の要因や要素で視覚的に周期性を補う必要がある.もともと数詞による順序数には,記数法で定められた桁上がりという周期がある.しかし,単調な繰り返しだけに,リズム感に乏しい.変化と周期性を同時に持ち合わせている数学的モデルには魔方陣がある.この概要は「魔方陣-複合的対称性-」のページを参照されたい.順序,乱数,魔方陣.これらの3つの数字配列は造形構成,あるいはその認識の為の基準となる特徴的な数学的モデルである.なお,ここで言う順序のモデルは,下記の図2のように関数による変換を含めた概念が含まれる.つまり,造形において移行,回転,拡縮に限らず,ベクトル的な変換は,変形プロセスにおいて時間的差異を形成し,時間軸と直交する断面的空間の中で,順序的事態を想起させるからである.したがって,乱数や魔方陣によるリズム化は,順序的なリズム現象の順序交換によって,同時性のなかに折りたたまれた時間を図2のように形成できる.変位の可視化とは,異なる世代の共存的表現でもある. このような配置と変形による複合的な効果を整理するには,量的にも記号的にも解釈できる数の配列概念が有効となる.多次元な要因をもつ要素の相互関係を多面的に統合できるからだ.現在のCGソフトは,配列変数により,点,線,面,立体(空間),タイムテーブルなどの構成要素を記憶し,加えられた要因によってそれらを変換処理し,要素の属性や環境条件に準じたレンダリング処理が行える.これらの配列概念に,リズム,シンメトリー,プロポーションの要因を加えると,形の構成をより高次な認識レベルへと導くことができる.もちろん表現とは受け手があって初めて表象が形成される.したがって,造形構成によって,受け手側の視覚的認知がどのような視覚的イメージを想起させ,その対象の解釈に至るかが重要なデザイン的課題となる. 参考文献 [1] “美の科学遊びーMagic Tiles” 形の科学会誌 22,11-12 2007 |
|
|
|
アルスノート研究所 / 研究紹介 / 研究内容
更新:10/02/15
>
12/07/13
|
| |
||