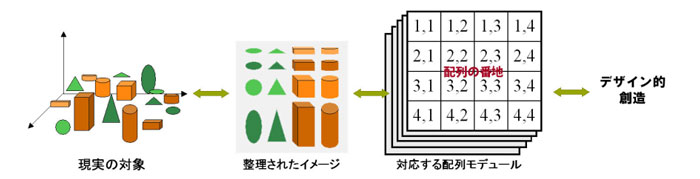
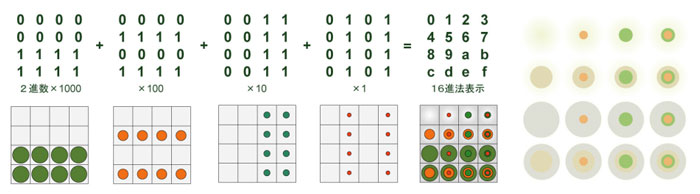
シンメトリーと動的バランス　　 この地上において形の秩序と無秩序をおおよそ見分けるには，同じ形の存在，つまりシンメトリーに注目するとよい．細波や鱗雲のような並進対称，雪の結晶や花のような回転対称，動物に見る左右対称などは，内在する秩序と外界との関係の表れだからだ．なんとも複雑な秩序をもつ生物も，重力の影響を受けにくい液体中に生じ,ほぼ球対称から外見が変化していく．重力によって上下を創るもの．螺旋に分裂して堅固な殻を形成するもの，動的に上下左右の対称性を保ちながら前後の差異を形成するもの，陸上に上がり,重力に打ち勝って静かに螺旋的分岐で繁茂するもの，左右の対称性を保ちながら疾走し，明確な前後と上下を形成するものなどが,抽象的パターンとして見出される． しかし，シンメトリーをもつどのような動物であれ，足やヒレを完全に左右対称に動かすことはまれだ．重心移動により対称性を自ら破らなければ，前進もままならないのであるから,対称性は一対の動的非対称から対象性を周期的に生み出す構造をもつわけだ．これは正に波動的前進である．面白いことに造形表現において，静的な図解や極端な象徴性を除けば，生物の輪郭を左右対称に描くことはまれである．通常は斜めから描き，顔を正面に向ける場合でも体のポーズを非対称にとる，あからさまなシンメトリーの構図を避けているわけだ．それではなぜ形を考えるときシンメトリーが重要に思えるのだろうか？それは脳の視覚認識において，明確なシンメトリーの概念モデルとの照合が成されているからであろう．どのようなポーズをとっても，脳内ではその状態の対応関係が，はっきりと左右対称の形を基準にバランスの程合いを把握のできるのである．そう考えると，地上の動物の前後や上下の差異はシンメトリーの乱れと言えるだろうか？運動中の対称性が崩れれば前のめりや尻餅をついて転倒するはずだ．ならば，ここにもモビールの腕ように力学的モーメントを保つ大地との絶妙な動的対称性が働いているはずである．周期性を伴った運動感覚も，シンメトリーの移行的変異＝リズムと考えれば，ますます形のシンメトリーとリズムは，切っても切れぬ深い関係にあることが推察されるであろう．

配列概念　ではここで，複雑な対称性を把握するための概念モデルとして，簡単な配列を使い，図 8で実在の形との対応関係をイメージしてみよう．

　図 8：現実の対象と整理されたイメージ．配列モデュールによる概念的操作がデザイン的創造性へと導く．

　上の図のように，現実がどんなに雑然としていても，脳内では，整理されたイメージに整え，更に対応する配列的抽象概念によって各要因を多次元的に抽象化することが可能である．この抽象としての配列モデュールは，表計算ソフトのように，配列要素ごとに現実の対象に対応するためのデータ・アドレス（添字）を定めることで表現できる．オブジェクト・データ，色データ，質感データなどの配列モデュール，およびリズム，シンメトリー，プロポーションのモデュールが格納され，さらに,空間構成のための移行，回転，拡縮データなどが含まれることになる．オブジェクト・データは，関数で表記しても良い．この配列モデュールの計算結果を更にベクトル変換することもでき，離散と連続を組合わせた様々な造形構成ができるわけだ．もちろんこれはコンピュータプログラム上での説明である．日常の認識の中では,数値化など飛び越えて頭の中のイメージでこれを操作しているはずである．したがって,いきなり手なりのスケッチが描かれてしまうのだ．認識の形の秘密を探るには,この無意識に処理される抽象的概念操作を意識することが必要なのだ．　

　では，このような配列による抽象化の中で，シンメトリーについて考えてみよう．


表 3：　順序化した4×4の配列とその順序交換．4進法2桁に変換するとリズムの頁・表1となる．

順序と周期のシンメトリー　まず，表 3左端のように2次元の配列に左上から右下に添字のように順序数を配置した．ここでリズム的な順序数でなく，量的な集合数としてのバランスを考えてみよう．上下・左右に２分割し４つのセット内の和は，10，18，42，50となり，和の対称性はない．右隣の2番目の配列は，左の配列の右端の列を左端に送って順繰りに右へずらしてある．上の２セットは和が14，下の２セットは和が46となり，全体として左右対称に近づいている．3番目の配列は，更に左の配列の下端の行を1行目に上げてずらしたもの．これはどのセットも，対角方向の和も30となり点対称に近い．では，一足飛びに右端の完全方陣を見てみよう．4つのセットの和も，行も列も斜め対角方向のセットの和も30となり，この配列は，なんと行や列を順送りしてもバランスが崩れない．まさに量的なシンメトリーの極みである（完全方陣の概要は魔方陣の基礎を参照）．したがって，順序化した配列から完全方陣の配列の間にはさまざまな構成が想定でき，バランスが整うにつれてリズムとシンメトリーが表裏一体で強化されていくのがわかる．分割されたセットの中では，同一性に注目すればシンメトリーが見え，変化に注目するとリズムが見えてくる． 表3左端の配列の0~15を4進法2桁に変換すると，リズムの頁・表1左端の4進法2桁の配列になる．16種類を4種に分けるには桁上がりの周期を変えるだけでよい．進数で割るごとに，各桁に余りを記せば変換できる．分割されて周期が短くなれば対称性は増し，折りたたまれていた順序の流れが各行各列の周期に修まったように見えてくる．


図 9：　2進法の各桁を配列ごとに分けて表示．0は白地，１は●で表した．●は桁によって大きさを変えた．

　更に2進法4桁に変換すると図9のようになる．各配列のシンメトリーを見てみよう．リズムのもつ移行的変位のバランスはシンメトリーで把握できる．配列の順序（添字）にしたがって左上から右下に読み進めれば，1桁目のパターンは0と1を交互に繰り返し，左端の4桁目のパターンは後半にのみ１が集まっている．平面的配置として見れば2桁目も同じになる．この周期性は図10のような波動と見ることもでき，図9は，面的に広がった反応拡散のような周期性にも見える．


図10：　0からf（15）の周期を波動的に表した．この重なりを視覚的に直感するのは難しい．

　魔方陣の基礎概念・図11は，完全方陣を2進法4桁に変換したものである．各桁の0や1が左右対称または点対称に並びバランスがとれているのがわかる．行や列を順繰りに入れ替えてもバランスが崩れない理由がパターンからも推察できるであろう．順序の配列と完全方陣の対比で構成の両極が定まる．イメージに沿ったその間の抽象的構成が想定される．

参考文献　「複合的対称性に関する構成モデュールと配列表現」　 形の科学会誌　2006．03
　
<PageTop>