更新:
20/08/19
,
|
|
プロポーションとハーモニー それでは,造形譜の構成のためのプロポーションのモデュール,つまり建築学的な「比例を生み出すシステム(あるいはアルゴリズム)」について見てみよう.図 5-4 のアイコンは,縦横が2倍になってゆくタイル状の要素のプロポーションを4×4のモデュールのアイコンとして示している.
図 5-4: 図 5-4: 四角錐をタイル状に並べた要素によるプロポーションのモデュール. リズムの基礎概念・図 5-2 と 図 5- 5 のアイコンによるイメージ・チャートを縦方向に見ると,構成のリズムが一定で,要素のプロポーションの違いが見える.さまざまなプロポーションのイメージ・チャートを作ることで,プロポーションとハーモニーに対する認識が深まるはずである. 下図中の上2段は、等差の整数比、下2段は、フラクタルスケールからの比となっている.
角度のプロポーション イメージ・チャートの要素とした四角錐は,真上から見た稜線が見かけ上の対角線となって見えている。その画面上の傾きは,tanα= 縦/ 横で,αに準じた角度のプロポーションを形成する.図 5-3 は,指定されたプロポーションのアイコン内に表れる対角線の角度を集めた図である.対角線が見えない場合でも矩形の対角線方向の印象は強い.このように視覚認識はかたちに惑わされずに流れを読む力もある. 比例と和の問題点 少々難しい問題であるが,図 5-2のプロポーションは等比級数,図5-5のプロポーションは2組の和を考慮した整数比になっている.地と図,量感と空間のプロポーションの調整には,実は音楽の平均律のように悩ましい問題が潜んでいる. プロポーションのモデュールの応用例 イメージ・チャートを作ることで,比例値がひらくほど対比が強まり,より繊細な雰囲気が感じられるのがわかるはずだ.プロポーションとイメージの関係が全体的につかめていけば,自分の好みのプロポーションを探し出すこともでき,感じるイメージの違いを,自分の言葉で対応づけながら認識を深めることもできそうだ.客観的変化に対応する主観的イメージを位置づけることで,図 5-6は,プロポーションを規定した応用例である.果たしてプロポーションのモデュールによる調和が感じられるだろうか?  図 5‐6 : 建築的要素をプロポーションのモデューで展開した作例. [プログラミング:笹田晋司,造形譜:石垣健, 2007] プロポーションは,度量衡のような客観的測定方法で定性化・定量化ができる.また,定性化,定量化の難しいフォルムや色彩,質感あるいは動きなどは,イメージとしての対比により順序化(正規化)をすることでモデュール化ができる.数理なら多項式の係数や定数に好みのプロポーションを与えてもよいわけである.プロポーションとは,あくまでも感覚的なものであるので,客観的数値と感覚的度合いとの補正が必要となる.水ですら温度によって個体,液体,気体と様相が変化する.ましてや,人間の感性が一様であるはずがないのでまことに面白い. 図 5-7は,放物線の変換による作例である.係数の変化だけでなく,配置,凹凸,大きさ,傾きなどのプロポーションのモデュールが加わってリズムを調和させている.  図 5-7: 造形譜「春相記譜」より 放物線を使った構成.右端のレリーフはNC切削で雌型を作成した. 情報密度自体にもプロポーションが… 面白いことに,関数の特徴(ここでは放物線)はそう簡単に消えるものではない.それは人間のパターン認識がいかに優れているかという証しでもある.絵画が絵筆で描かれる以上,実に複雑な線形ベクトルと離散的要因により形成されていることを想定できる.だが,享受する側は,注視した対象を詳細に見分けるが,それ以外は空気のごとく読み飛ばすこともできる.フォルム,リズム,プロポーション,どれを欠いても単調となりがちな表現だが,なんともその描き込みの加減は難しい.これもまた情報密度のもつリズムとプロポーションの作用である.
<PageTop> |
|
|
|
アルスノート研究所 / 研究紹介 / 研究内容
更新:10/02/15
>
20/08/19
|
| |
||




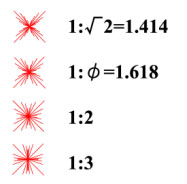 図 5-3:角度のプロポーション
図 5-3:角度のプロポーション 