アルスノート

　 イメージ
　 　生まれたときから大森近辺に住む者にとって，海は埋め立てで遠くなるばかりである．昔は，省線（JR）の大森駅前で前採れのカニを桶に入れて売っていた．海から天秤棒で担いでくるのだ．空き地には海苔も干してあった．家に二階はなかったが，どこの二階屋からも海や富士山が見えていたものだ．そんな海への郷愁，遠くなった海を足元へ寄せたかった．気が付くと海が座っているスケッチになっていた．海の静かな帰還である．

　寸法のモデュールについて
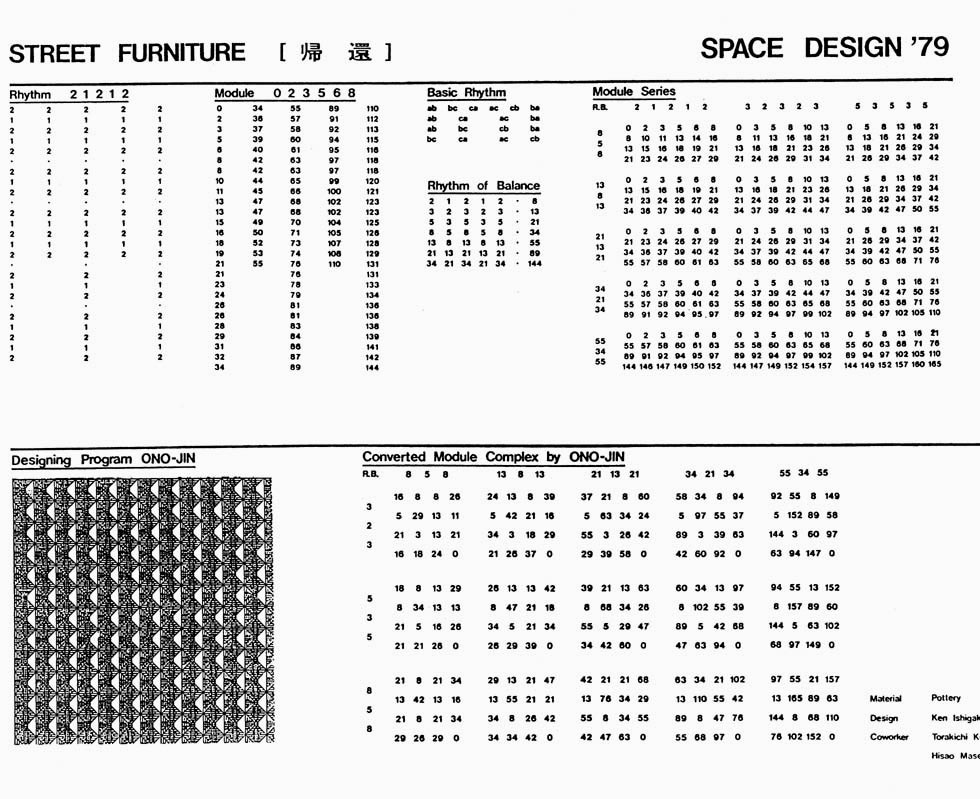
　造形における比例のモデュールとはユニットとファクターのプロポーションを統合しハーモニーの基盤を整えた数理的モデルである．この作品に使用した比例のモデュールは，生み出されるプロポーションに黄金比とその仲間を加えたもので，フィボナッチ数列を基準とし，完全方陣のリズムに対応変換可能なモデュール “Self-similar Module” とした一例である．これらを寸法のモデュール “Self-similar Scale” として使用することで，黄金比とその仲間が組見合わされ，アナログ的な視覚的比例関係の対比とデジタル的な寸法の和の一致が一体となり，完全方陣をモデルとした配列の利用も可能となる．

　基本としては，１から１４４までの整数で，比例関係を調和させるので，初項に近い比例には揺らぎがある．それ故に記譜としての概略的指定が制作時の工夫につながる．寸法のモデュールとして　１point ＝１ｃｍとすると十分実用的だ．大きな節目の寸法が意味を持つように作品に合わせて見立てていける．もちろん，固有の表現のためには固有の比例モデュールが作れるシステムとなっている．

　 造形とは自然の模写だけではない．人間の感性を如何に拡張させて美しい人工物とするかという試みでもある．それには，イメージを抽象化することで調整し，その記譜（当時は寸法モデュールを記入した手書きのスケッチ）により，構法を含めた構成の再解釈を行い，具体的な製作図や原寸モデルを作成した．焼き物の場合は，前作同様に型からの再解釈により，素焼き，釉薬，本焼きでの調整が行われている．

Sketch and "FRACTAL SCALE "　on a ruleｒ.

作品の平面スケッチと「フラクタルスケール」
フィボナッチ数列を基準とした自己相似モデュール （Self-similar Module）
による物差し「フラクタルスケール」を作成・使用した.
これ以降、私は、ほとんどの作品でこの「フラクタルスケール」を使用している．
尚、「フラクタルスケール」のネーミングは2018年から使用することとした．

　展示パネルの写真に当時の研究者達が共通に使用したＲｈｙｔｈｍという用語があるが，いま振り返ると，これはProportionを生み出す基本的比例（Basic Proportion）と考えた方が妥当である．したがって，これらの比例を生み出すモデュールは，選択的に使用する方が特徴が現れやすく，善し悪しはさておき認識しやすい．ご覧の様に、このモデュールでは基本的比率が1対２であるが、やがて黄金比に収束する。もちろん、派生的に生じる比例を自由に選択可能となる．自己相似化は、全体や部分の関係を自由かつ的確に位置づける手助けとなるはずだ．

　 Rhythmという用語は，ポリリズムのような空間的広がりを持つ配列的認識やその指定に対して使うべきだろう．序列化においては，我々は文字や記号による順序付けの記憶があり、それらのアプローチは容易であるが，バランスを保つ完全方陣は特殊なリズムであり，構築が難しいので記憶やメモを必要とする．だが，これも配列を覚えてしまえれば、順序の記憶と同等の情報となり、何の困難もない構成となる．つまり，１，２，３…や、ABCといった誰もが記憶している順序とは，構文から見ればリズムの特異な状態に過ぎない．リズムは移行的変位であるから、比例を併存させることができるので混同するが、そこが面白さでもある．　ｉｓｉ


参考文献：上記のモデュールを作った1979年頃には，黄金比の文献は主観的で，科学的と言える解説が見当たりませんでした．近年，とても冷静で，多くの文献を参照した著作が出版されていたので，以下に紹介させていただきます．
　マリオ・リヴィオ著（２００２）　斉藤隆央訳 「黄金比はすべてを美しくするか？」 　最も謎めいた「比率」をめぐる数学物語 2012　早川書房　

原著
THE GOLDEN RATIO
The Story of Phi,the World's Most Astonishing Number
by Mario Livio 2002

第8章　タイルから天空まで　／　フラクタル　に書かれている2進法表記の０と１を１と２に換えて，対称性をもつ周期で区切ると，上記の「Self-similar Module」と同型になります．さすがに宇宙物理学者の説明は明快ですが，視覚的には，対称性からフラクタル的構成を見いだす方が解り安いですね．
　 長生きしてみるもんです．素晴らしい著作に　感謝！　isi　追記：2019/01/23, 2020/7/25